Spoilers and Spite

Ah, the wonders of plurality-based voting. New York's 20th congressional district is having a special election, after their congressperson, Kirsten Gillibrand, was appointed to Hillary Clinton's senate seat (after Clinton became Secretary of State). It's a slightly-Republican-leaning district, but Eric Sundwall was running as a candidate for the Libertarian party. The Libertarians, of course, when compared to the two major parties, are most-similar to the Republicans, and so, thanks to plurality voting's susceptibility to spoilers, would likely have siphoned more votes from them than from the Democrats.

The Republicans in the state apparently felt that Sudwall's spoiler-effect might have been strong enough to sink the candidate's, Jim Tedisco, chances of wining, and so launched a coordinated effort to challenge Sundwall's petition signatures, and force him off the ballot. They were successfull. And so, Sundwall has endorsed the Democratic candidate, Scott Murphy. Tedisco's campaign is already considered to be much more negative than Murphy's, and this can't be helping.

Sundwall was only showing about 2% support in the election, with approximately equal support from Democrats and Republicans, so you have to wonder how much the Republicans thought this would help them. But in a close enough plurality election, a spoiler only needs a couple of votes to change the outcome. Under instant runoff, a candidate needs at least 25% support to spoil an election, and under score voting, spoilers don't exist.

A Glossary (For Terril Bouricius)

Like any field, discussion of voting methods has developed a language all its own, full of jargon and technical terms that, while clearly defined for those well-versed in the field, are sometimes confusing or completely opaque to those on the outside. So I don't fault Terril Bouricius for his repeated failures to understand the lingo. I hope he will find this short glossary of voting-method terms useful.

non-mon·o·ton·ic: adj. 1. In reference to a method, a property meaning it is possible in that method to construct a scenario where either a. by improving a winning candidate's rank (or score) on some ballots, the candidate becomes a loser, or b. by lowering a losing candidate's rank (or score) on some ballots, the candidate becomes a winner. 2. In reference to an election, an example where either of the scenarios in 1. is in evidence.

spoi·ler: n. 1. A a non-winning candidate such that, if they are removed from all ballots, the winners of the election change.

By these well-accepted definitions, instant runoff voting is a non-monotonic method (whereas score voting and even plurality are monotonic), and Burlington's recent mayoral election was non-monotonic; instant runoff voting is susceptible to spoilers (plurality is too, but score voting is not), and Kurt Wright was a spoiler for Andy Montroll. These are easily-proven, in-arguable facts, and so are not up for discussion. So please, stop arguing from a position of ignorance, and learn the definitions.

Non-Monotonicity: Part II

In Part I, we defined non-monotonicity, showed that Instant Runoff Voting is a non-monotonic voting system, and that the recent mayoral election in Burlington Vermont suffered from non-monotonicity.

Here in Part II, I'll talk about why monotonicity matters, and do my best to refute all arguments to the contrary.

What happened?

To understand why it's important, first we should try to understand what happen to make an IRV election display non-monotonicity; we'll use what happened in Burlington's IRV election to showcase. I mentioned that "monotonicity" is an idea borrowed from algebra, but let's make that more clear: rather than move just 8 votes from Wright to Kiss, as we did in the example in Part I, let's make a function out of it, so we can see what it's like to move any number of votes over, and graph it against the vote-tallies in the final IRV round. A picture should make this clear:

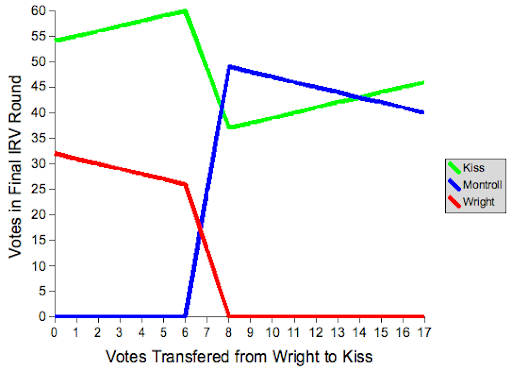
You can see the huge discontinuity at 8 votes, where the IRV algorithm changes which candidate is eliminated. You can also see that, at 14 votes, the election switches back into Kiss' favor. So there's a limited window where this sort of manipulation will work. Foremost, obviously, is that there must be at least three candidates in the election. As candidates are eliminated, when only three are left, they must each have more than 25% of the vote. Finally, the eliminated candidate (the one with the fewest first-place votes) must be the "beats-all" (or "Condorcet winner") candidate, meaning that, in any one-on-one race, they would win. We can determine this by, for each pair of candidates, removing all but that pair from every ballot, and seeing who would win. For the Burlington election, check, check, and check.

Under these circumstances, IRV exhibits non-monotonic behavior, and eliminates the Condorcet winner. In fact, you could say that because it eliminates the Condorcet winner, it has exhibited non-monotonic behavior. But so what? Well, there's a hidden implication in the elimination of a Condorcet winner, and that is that the Condorcet winner is the moderate candidate, the compromise candidate. Meaning that, by eliminating them, we've chosen an extremist candidate.

In the Burlington election, in addition to the nationally-familiar Democratic party (with candidate Andy Montroll) and Republican party (with candidate Kurt Wright), we also had the eventual IRV-winner, Bob Kiss of the Vermont Progressive Party, which is just a bit more left-leaning than the Democrats. There is a model of voting behavior, appropriately refered to as the "1D" model, where candidates and voters are arrayed on a line, left to right, and voters always more-prefer the candidate closer to them. In the 1D model then, we should expect that all Kiss-first or Wright-first voters would have had Montroll second (ignoring, for now, candidates other than these three). And that's almost the case: among those who expressed a preference, Wright voters prefered Montroll 3:1 over Kiss, and Kiss voters prefered Montrol 7:1 over Wright. 1D isnt' perfect, but it's often pretty close (how much of this is feedback from our two-party dominated political process is an article for another day), and in my "simplified" example of the election, I moved all the "wrong" votes to their "proper" 1D vote. If the purpose of an election is to choose an appropriate candidate to represent a body of people, it's logical to say that you want the winner to come from the center of the spread of voters' opinions; it's a compromise.

But IRV doesn't always pick the compromise candidate; instead, it picks one of the two extremes. The Center for Range Voting has some excellent graphical representations of this, using a 2D political spectrum and many more candidates (which is more realistic than our 1D, 3 candidate example). At a glance you can see how extremist candidates encroach on the territory of more moderate candidates.

On one hand, it's very strange for me to be damning this election, since it technically elected a third-party candidate, which I generally find to be a good thing. One of the reasons I find our current system so abhorrent is because third-party candidates actually damage their most closely-aligned major-party by acting as spoiler candidates. On the other hand, that's what happened in Burlington. Nearly two-thirds of Burlington residents are registered Democrats (click "voting" on that page to expose the data). And considering the Democratic wave that has been washing over the nation recently, in a vote between right, left, and lefter, the Republicans are the "third" party in Burlington. And as a third party, they operated as we would expect; they siphoned votes away from their nearest major-party candidate and gave the election to their most-hated opponent. Their nearest major-party candidate just happened to be the Democrats.

The "third party" Republicans opperated as a spoiler. Under the 1D model (and by a 7:1 margin in actuality) they would prefer the more-moderate Democrat, Montrol, over the further-left Progressive, Kiss. But their votes for Wright acted only as votes against Montroll in the final tally. This is exactly analogous to Nader spoiling Gore. Despite IRV proponents claims, IRV does not eliminate the effect of spoilers, it only delays their effect. Under our current plurality system, spoilers can have an effect with as little as one vote, if the other candidates are close enough. Under IRV, they only pop up when they have at least 25% of the vote. But the effect will ultimately be the same: fear of spoilers will tend to drive voters back towards the two major parties.

Both of these things—failure to elect a "beats all" winner and susceptibility to a "spoiler" candidate—are indicated by IRV's non-monotonic behavior. Non-monotonicity is the smoke to their fire, or the chink in the armor that lets them sneak in. As IRV advocates will claim, it doesn't matter that if some voters changed their votes they could change the outcome in a non-intuitive way; because they didn't. It matters because that possibility indicates that elections will tend toward extremism and towards two-party domination.

How often?

After being forced to admit that, yes, non-monotonicity is something to be concerned about, an IRV advocate's second round of defense will be that it doesn't matter because it doesn't happen that often. And I must admit, this one example is just one example; the plural of "anecdote" is not "data". Luckily, a host of very smart individuals have tried to calculate how often these things should happen, which CRV has taken the time to summarize. The first to make the attempt was Crispin Allard in 1996, and he calculated the chance as 1 in 40,000, and this is the number upon which IRV advocates have built their argument. Unfortunately, Allard's calculation was wrong. Very wrong. He only counted the more common of the two types of non-monotonicity, and he took advantage of a six-fold symmetry to simplify his calculations but forgot to multiply by six at the end, but worst of all made a serious arithmetic error. Over all, he was off by a factor of over 1,000.

Corrected calculations have found that, using Allard's model and his assumptions, the correct odds of an IRV election displaying non-monotonicity is closer to 1 in 7.

But, an IRV advocate might say, that's only one model. Yes, it is. Using a different model, the odds were calculated to be around 1 in 18, and in a third, a little less than 1 in 10. That, combined with the growing list of real-life IRV elections that have displayed non-monotonicity, it should be quite clear that these failures are predicted to happen often, and often happen in real life. Also, it's important to note that these values apply only when there are three strong candidates in a race. As the number of viable candidates increases, the odds only get worse, until the chaos is practically guaranteed.

What's it mean?

Ultimately, adoption of IRV will result in practically no change to the status-quo. Third parties will find they can gather more votes, but they still won't be able to win any elections, because of the fear of spoilers. Voters will still find themselves deciding between the least-evil of a pair of party-chosen politicians, and we'll continue to lurch back-and-forth between left-leaning policy and right-leaning policy, rather than pick a stable course. The divide between "red" and "blue" will continue to grow and our common ground will continue to wither away. And let's not ignore that this non-improvement comes at a high cost (another post for another day). Why not focus on a change that will actually change something?

I've come down hard on IRV here, but that's only because it's the loudest competitor. The truth is, every election method that uses ranked-order ballots (i.e., ballots of the type A > B > C) is susceptible to one of two failings, either "favorite-betrayal" (which IRV displays through its non-monotonicity) or something called "cloning" (which, briefly, involves proping up ideological copies of your opponent in order to split the votes of those who oppose you). IRV is immune to cloning, a fact that they proudly showcase in this video, while ignoring their non-monotonicity pitfall. ("Or something like that" indeed!) Now, cloning is a serious concern under our current plurality system; but why fix one problem by introducing another, when score voting is clone-proof and monotonic, not to mention cheaper to implement?

Commercial Interruption

On a whim I added some links to the blog front page (over to the right there), and wanted to add a link to "Gaming the Vote" (which I reviewed a few months ago.)

Well guess what; it looks like the hardcover version is currently selling for just five dollars! If you haven't already read it, buy one today. I'm thinking of buying one for my town councilman, and one for the mayor, plus one for my state representative, another for my state senator, one for my U.S. representative, two for my U.S. senators... you get the idea.

In addition, currently the top-rated customer review is from Mr. Terrill G. Bouricius, the well-known Burlington Vermont resident, IRV advocate, and IRV software-seller I mentioned just the other day. Since Poundstone ultimately comes down in favor of score voting (AKA range voting), Bouricius gives him a 2-star review (point of irony: Amazon's 1- to 5-star ratings are effectively a score voting system.) Bouricius mentions Nicholas Tideman's dislike of score voting (a link to his book (a smidge pricier), CRV's review and follow-up responses.) Which is an issue worthy of a blog post in its own right (after I finish discussing non-monotonicity.) Anyway if you have read the book, I encourage you to write your own review/rate the existing reviews.

Non-Monotonicity: Part I

Since the results of Burlington's mayoral election were announced, battle has raged across the internet between advocates of instant runoff voting and those who have better ideas. Several points are being argued discussed, but the most confusing in the issue of non-monotonicity. What's that word even mean?

Monotonic, if you remember your algebra, means that a function, f(x), is either always increasing or always decreasing as x increases. A function that goes up for a little while and then goes back down is non-monotonic. You could think of it as "if more is better, than even more is even better". And that's (sort of) how the analogy comes over to voting methods: under a monotonic method, getting more votes is always better. So under a non-monotonic method, getting more votes is sometimes bad, or, getting fewer votes is sometimes good.

There are three issues at stake here: first, is IRV non-monotonic? This is an unqualified "yes", although IRV advocates will claim that it's so rare as to be inconsequential in real-life elections. (More on that later.) Second, did the recent election in Burlington exhibit non-monotonicity? This is also an unqualified "yes", which one might think would give pause to those claiming that non-monotonicity is ultra-rare. (Rather, they have decided to argue that it didn't really happen.) And finally, does it matter? This is the only issue of the three which can be up for debate, which we'll do in Part II. But first, we'll pause to prove points one and two.

IRV is non-monotonic

The easiest way to show this, is to construct an example. First, the election needs to have at least three candidates; let's call them 'K', 'M', and 'W'. Secondly, we need to construct a set of ballots where one candidate, let's pick K, is the winner, but in such a way that if we improve K's ranking on some of the ballots, they instead lose. Easy enough:

29 ballots: K > M > W
25 ballots: M > K > W
32 ballots: W > M > K

M, with the fewest top-ranking ballots, is eliminated, and K defeats W by an impressive 54 to 32 margin. But! if we improve K's position on just eight ballots, like this:

29 ballots: K > M > W
25 ballots: M > K > W
24 ballots: W > M > K
8 ballots: K > W > M

Then instead candidate W, with only 24 top-ranking ballots, is eliminated, and M defeats K by a 49 to 37 margin. To repeat: by improving K's score on a small number of ballots, K went from being the winner to being the loser. Which is a very non-intuitive result. It's also possible to create a situation where decreasing a losing candidate's rank on some ballots can cause them to win (but I leave that as an exercise to the reader). If either of these cases is possible to construct for a given voting method, then getting more votes is not always better, and by definition the voting method is non-monotonic.

What about Burlington?

So clearly these situations can happen under IRV. The next question is if the Burlington election was one of those situations. The proof of this is almost trivial, since the numbers (and names) in the above example were pulled from the results of the Burlington election (with a few complicating but non-relevant omissions.)

The real question is, why do IRV's supporters insist that this is not the case? I wish I knew! It seems to stem from a lack of understanding of the words "if" and "could", as in "If the outcome of the election could be changed by...", as their argument is that this election "could" have been non-monotonic "if" some voters changed their ballots "but they didn't". No, no, no! If they could then it is non-monotonic! A lot of bad-blood is being spilled over this non-disputable point, and I don't understand why the opposition persists, as it only serves to distract us from the real discussion.

Which we'll cover in the next installment.

IRV Fails In Its Own Backyard

Burlington Vermont just elected their mayor, which wouldn't be big news, except that Burlington is the home town of one of IRVs largest proponents, Terrill G. Bouricius, and he has persuaded his town to use that system. Courtesy of the Center For Range Voting, we show how this election perfectly demonstrates the problems that IRV causes; the ones that Bouricius and Fair Vote insist are "unimportant", "unlikely", and "uninteresting". Namely:

• Failure to elect a majority winner: the eventual winner, Bob Kiss, would have lost to Andy Montroll in a one-on-one election. In fact, Montroll would have beaten any other candidate in a one-on-one election.
• Failure in the face of a spoiler candidate: if Wright hadn't been in the election, then Montroll would have won.
• Failure of participation: if a few hundred Wright voters had stayed home and not voted, they would have gotten a better outcome (their 2nd choice, Montroll, instead of Kiss.)
• Failure by non-monotonicity: if a few hundred Wright voters had instead voted for Kiss, Kiss would have lost (and Montroll wold have won).

The first, I can almost forgive; it's not as if Condorcet's method is perfect either, and IRV advocates can make a deliberate choice between simplicity and effectiveness. The second makes me furious, as IRV advocates prey on Democrat's fear of Gore-Florida-2000-like scenarios, claiming IRV will completely fix problems with Nader-like spoilers; but this election exemplifies how this is not the case. The third, considering the already embarassingly low voter turnouts in the US, is disgusting; we cannot allow people another excuse to stay home on election day. Finally, "non-monotonicity" gets brushed off by IRV advocates as being too "academic" to be concerned over; sure, it's a somewhat complicated concern, but it's a serious concern, which this election shows.

Considering all these failures--all the ones that the Center for Range Voting has warned about and Fair Vote has repeatedly brushed off--I'm disgusted that Fair Vote is pretending everything is fine. Why--how--could you continue to support IRV in the face of this overwhelming evidence from your own home town? Is it ego? Or maybe... it's the money? Yes, in addition to being a "senior analyst" for Fair Vote, Mr. Bouricius is one of the founders of Election Solutions, Inc., who sell the software that Burlington uses to run its elections.

Honesty is the Best Policy. But...

Warren Smith's mamoth voting study in 2000 (abstract, pdf) revealed several exciting bits of information. Chief among these was that score voting (referred to as "range voting" in the paper) had, under all 700+ conditions, the best performance of any voting method he examined. Less significant to the voting-reform movement, but no less interesting, was his finding that performance was better with a population of honest voters than with a population of strategic ones, for every method examined.

But what does "honesty" mean, in this sense? If your only voting experience is with the plurality system (which is likely), the idea of a dishonest vote might be confusing; after all, if you prefered Barak Obama, why would you lie and say you preferred John McCain (or vice-versa)? Of course you wouldn't; but maybe you would have prefered Hillary Clinton (or Mitt Romney or Mike Huckabee or even Ron Paul) or maybe even Ralph Nader. If you honestly, in your political heart-of-hearts, preferred one of these other candidates, but voted for one of the two front-runners, then you are a dishonest voter.

You are a dishonest voter

Or, to put it a nicer way, a "strategic" voter. After all, it doesn't take a genius to realize that voting for one of the other former Democratic (or Republican) candidates is a waste of time: there's a reason why parties have primaries, and it's because our election system provides strong incentives to reduce the election to a choice between just two options, so they better make sure all their people are backing the same candidate, ensuring they'll be one of those two. The same incentives are what cause our politics to be dominated by just two parties); in fact, voting for a third party actually makes it more likely that your less-preferred choice among the "major" candidates will win. This is a fact still warm in the minds of left-leaning Americans from Nader's spoiler effect in Florida in the 2000 pressidential race (or if you prefer, among right-leaning Minnesotans in the 2008 senate race.)

So: people--probably you--vote strategically in order to increase the effect their vote will have on the outcome. You don't vote for a candidate who "can't win", and only two candidates will be able to win. Now, back to Dr. Smith's experiment. His measure of performance is called "Bayesian regret", the idea being that we take all the positive and negative effects (commonly referred to as "utilities") that every voter would experience for each candidate if they were elected, add them all togehter to get society's utility, and for each election method determine how much worse the winner is when compared to the best possible candidate. Smith's results showed that, under every election method he tested, if everyone votes honestly (i.e., as truthfully-accurate to their computer-generated utilities as allowed by the election method), then the net utility for society as a whole is better. But we just showed that, at least under our current system, vast numbers of people don't vote honestly, as the system compels them to vote for "the lesser of two evils".

Why do people do that? We can answer that by examining these same utilities: if I honestly prefer Nader over Gore (utility of, say, +9 units versus +8), and Gore over Bush (+8 units versus -5), but realize that a vote for Nader will result in Bush being elected (as occured in Florida in 2000), then I can maximize my personal utility by dishonestly voting "for" Gore (really, "against" Bush.) But if everyone follows this sort of plan, then Smith's results show that on average, across a great many elections, society's net utility will be lower. (You might ask, "Why don't we just measure everyone's utilities, and determine the optimum winner that wasy?" The answer is simple: people will strategize ("lie") about those, too. (It's okay to use them in the simulation though, since we assigned each computer voter their honest utilities programatically.))

Strategy under score voting

What about Smith's election-method-shootout winner, score voting? Well, it turns out you can lie there, too. Maybe you have in your mind some "ideal" candidate, who agrees with you on every issue; but what if none of the candidates for office matches you on more than 70% of those issues? Do you give that candidate 70% of the maximum score? Or do you lie just a bit, and give them the maximum score, increasing their chance to win? Similarly, do you give your least prefered candidate a 0, or do you give them 20% because they agree with you on a few issues? What if everyone else was doing it? That's just the tip of iceberg though. If you really wanted to maximixe the impact of your vote, you'd look at the polls, figure out who the two front runners are, and give whichever of those two candidates you prefer and every candidate you prefer better than them, the maximum score, and give the other candidate and every candidate you prefer less than them a zero; if there's any candidates left, you could scale them appropriately to fit between those extremes.

No election method (short of deep mind-reading to determine real, honest utilities) will ever be immune to strategic manipulation. But score voting is hurt much less by it than our current plurality system; strategic score voting is functionally the same as approval voting, which was also examined in Smith's study. Indeed, those two methods have identical Bayesian regret with 100% strategic voters. Furthermore, there's less for a strategic voter to gain; the chance that a strategic vote will change the outcome is lower, and there's never any reason to give your honest true favorite less than the maximum score, a property called "immunity to favorite-betrayal". So you can feel good about yourself while still maximizing your impact on the election, by giving your honest favorite "third party" candidate as well as your favorite "major" candidate both the maximum score. Given some time for the party to grow support, a third-party candidate could even win an election; we can actually escape the two-party system.

Strategic IRV = Strategic Plurality

Interestingly, instant-runoff voting (IRV), which is gaining popularity following its adoption in several parts of California, is exactly the same (which is to say, exactly as bad) as our current plurality system when we assume strategic voters. IRV and plurality are analogous to score and approval in that sense: in the worst case, they're identical. And assuming a constant percentage of honest voters, score is always better than IRV as measured by Bayesian regret. This is because, while an IRV advocate will tell you that you can honestly vote Nader > Gore > Bush without fear, this is only true up until Nader has about 20% support. At that point, a vote for Nader will cause Bush to win instead of Gore, which means we will continue to be trapped in a two-party system. While IRV is (in someways) better than plurality, score voting can actually create some change, and means you can always afford to be honest.