What Do You Mean By "Best"?

Plurality voting is terrible and should be replaced, but what's the best voting system to replace it with? This isn't a new revelation, or a new question; for instance Thomas Jefferson considered the problem. But academic inquiries to it had been in a lull since Kenneth Arrow's Nobel-prize-winning work in 1950 showed that, given certain assumptions, there was no perfect system. Social-decision scientists everywhere were crushed.

What little debate that continued about the subject focused around various "voting system criteria". Arrow's work had shown that a group of five certain "clearly necessary" criteria were mutually exclusive, but perhaps by breaking certain ones in a minimally-damaging way an almost-perfect voting system could be found. The problem was, no one could agree which criteria were most important; each practitioner could always come up with some worst-case scenario in which their opponents latest new proposal clearly gave a horrible result (usually involving a candidate named "Hitler" winning the election, just to make the point clear.) And so the debate degenerated to what situations were more likely to come up or led to more damaging results: the terrible one I concocted for your new voting system, or the terrible one you concocted for mine. But all these arguments lacked one important piece: evidence.

To make good estimates of how often various worst-case scenarios happen and how bad they are, it would take at least hundreds of elections, each with a minimum of a few hundred participants, multiplied by each of dozens of systems that had been developed, in order to get a clear picture. But even then, what do you measure? When your experiment is to ask people "what's the best ice-cream favor," how do you measure whether the voting system was right without knowing the right answer ahead of time? And how would you determine the right answer ahead of time, without asking people to vote on it?

The problem is that economic utility can't be measured directly. Combined with the in-feasibility of performing enough test-elections, it's enough to make almost anyone throw up their hands in frustration.

But here's a clever idea: what if we replace real people with little bits of computer code? Instead of futilely trying to measure each participants utility, we can just assign them randomly from a statistical distribution. We'll have each little bit of code "vote" using every one of the electoral methods we've developed, but also calculate what the maximum possible utility could be from each election, and see how much we miss by. And we'll do it a few hundred times and take the average. Running the whole simulation should take maybe a long weekend. (If only Arrow had had access to a modern desktop computer!) What would we find? Let's ask Professor Warren D. Smith, who ran this simulation over the 1999/2000 New Year's holiday.

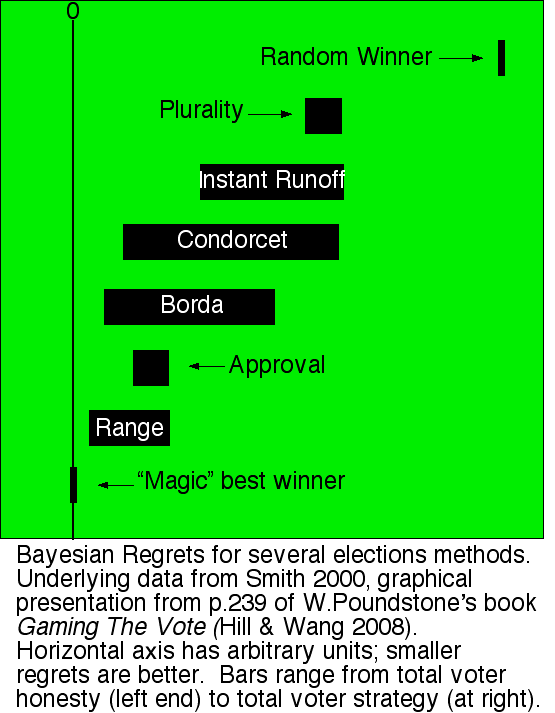
If the data from this simulation is to be believed, using approval voting, or score voting (listed here as range voting), could improve the results of our elections by the same proportion as voting at all is an improvement over choosing our leaders at random. That's an astounding result!

Of course, there are still critics: most of them just repeat their favorite criteria argument (usually later-no-harm or majority, since score and approval fail them) ignoring that this data already accounts for any downsides from those short-comings. A few smug folks point out that you can't measure utility; but we already know that, that's why we used a simulation. Some attacked the statistical distribution of utility (now we're getting to something meaty!), so a series of better distributions, based on their suggestions, were used: the results were virtually the same. Then they argued that voters are a poor judge of their own utility; so the experiment was rerun with a "voter uncertainty" parameter. Even with a 50% error factor, score and approval still top the list.

The most bizarre argument is that score and approval can't be the best voting systems, because they aren't voting systems at all. You see, one of Arrow's assumptions was that a voting system would convert a set of all voter's "ranked-order preferences" into a societal order of ranked preferences. But score and approval don't used ranked-order preferences; perhaps, if Arrow hadn't used this overly-restrictive requirement, it wouldn't have taken 50 years to find these results.

Not only is this an astounding result, it seems to be a fairly unassailable result. The "best" voting system is score voting, and approval is almost as good (but easier to implement).